wiki · home

Trees

A tree is a data structure that resembles an actual tree. It has a root node and from there other child nodes follow. The nodes at the deepest level are called leafs and they don’t have any child nodes.

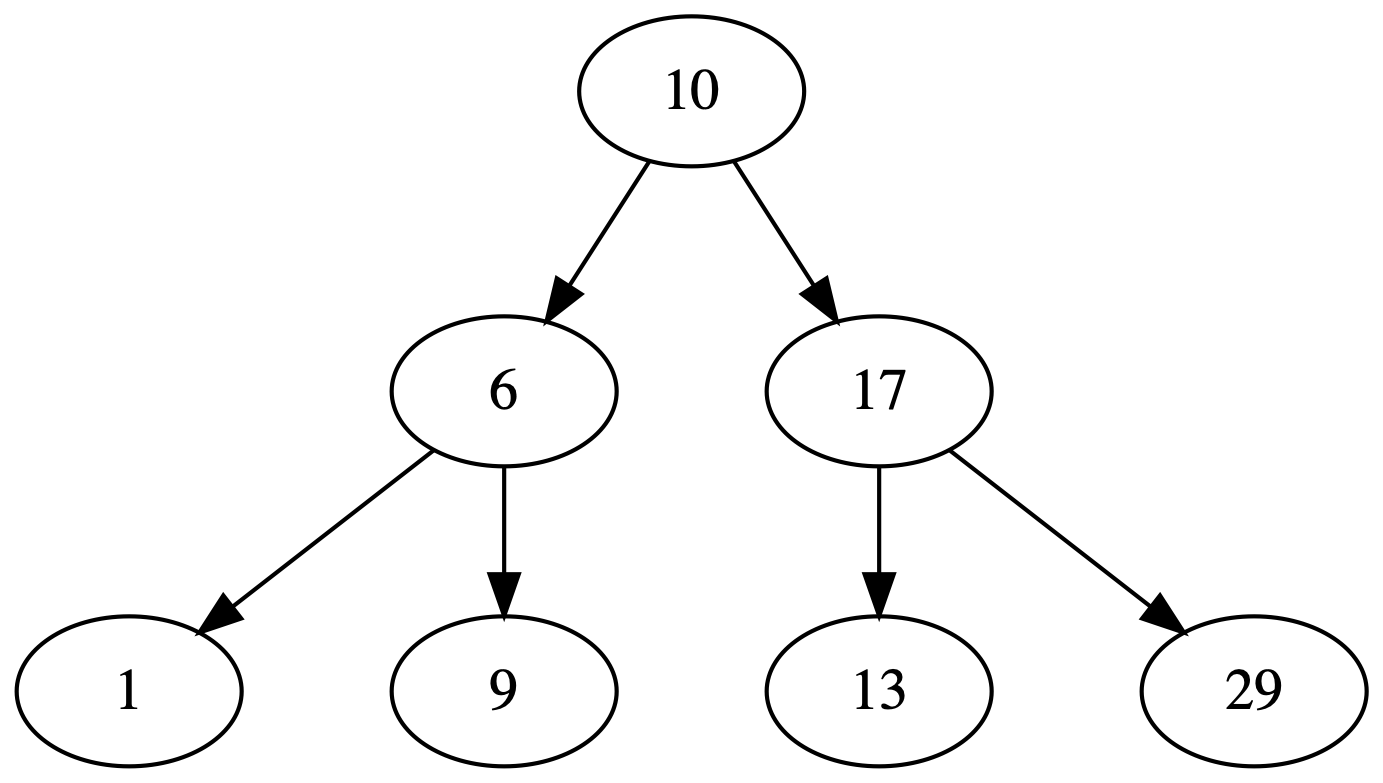
Binary search tree

Binary Search Trees

A binary search tree is organized in a way where each node can have at most two child nodes. Another characteristic of it is the fact that the left-hand side node contains an element that is less than or equal to its parent node. And the right-hand side node is greater than or equal to its parent.

if x.key <= p.key {
    p.left = x;
} else {
    p.right = x;
}

Walk orders

There are different orders to print the nodes in a binary search tree. The difference between them is when the current node is printed:

fn inorder(node: Node) {
    if node == nil {
        return;
    }

    inorder(node.left);
    println!("{}", node.key);
    inorder(node.right);
}

This operation takes O(n) time.

Searching a binary search tree takes O(h) time where h is the height of the tree.

fn search(node, k) -> Node {
    if node.key == k {
        return node
    }

    if node.key > k {
        return search(node.left, k);
    }

    search(node.right, k)
}

Minimum and maximum

These operations also take O(h) and it just needs to follow the same direction downwards until a leaf node is found.

fn minimum(root) -> K {
    if root.left == nil {
        return root.key;
    }

    minimum(root.left)
}
fn maximum(root) -> K {
    while root.right != nil {
        root = root.right;
    }

    root.key
}

Insertion

Inserting a new value in a binary search tree also takes O(h) time. The procedure is to follow the branches according to the new item’s key.

fn insert(root, n) {
    let y = nil;
    let x = root;
    while x != nil {
        y = x;
        if x.key > n.key {
            x = x.left;
        } else {
            x = x.right;
        }
    }

    n.parent = y;
    if y == nil { // root was nil (empty tree)
        root = n;
        return;
    }

    if y.key > n.key {
        y.left = n;
    } else {
        y.right = n;
    }
}

Deletion

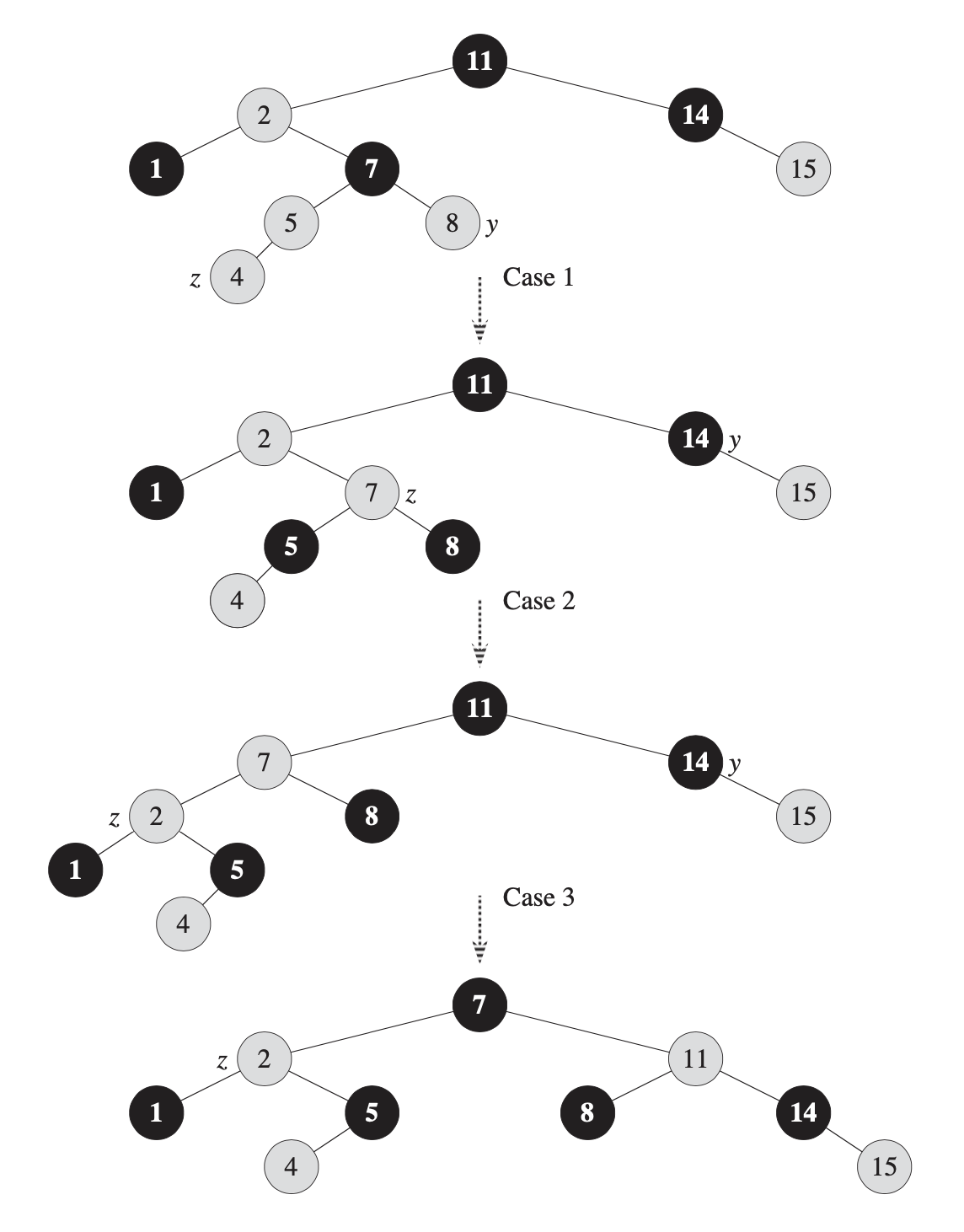
Removing an item also takes O(h) time and it’s more tricky than insertion in one case. When removing a leaf node n, all that it’s required is to remove it from its parent. When n has one child, its parent inherit the child node. The tricky part is when n has two children. In this case, we need to find the successor of n such that it is the smallest value greater than n.key. Then that node takes the place previously occupied by n.

Random Binary Search Trees

When the elements are randomly inserted; i.e.not following a specific order; a random binary search tree arises from it. In this type of tree the operations then take O(log n) time to complete. And that is also the expected height of the tree: log n.

Balanced trees

Self-balancing search trees not only preserve the search tree property but also maintain the height as minimal as possible. There are different types of such trees and each type has their own properties that need to be maintained in order to have a low height as possible. Some examples of such trees are: Red-Black trees, AVL trees, 2-3 trees, B-Trees.

Because the tree is always balanced, the operations then take O(log n). Whenever a new element is inserted or removed the invariants are checked and if any violation occurred then a re-balancing step is executed. This step is usually done by rotating the tree based on a pivot node.

Red-Black tree inserting node z

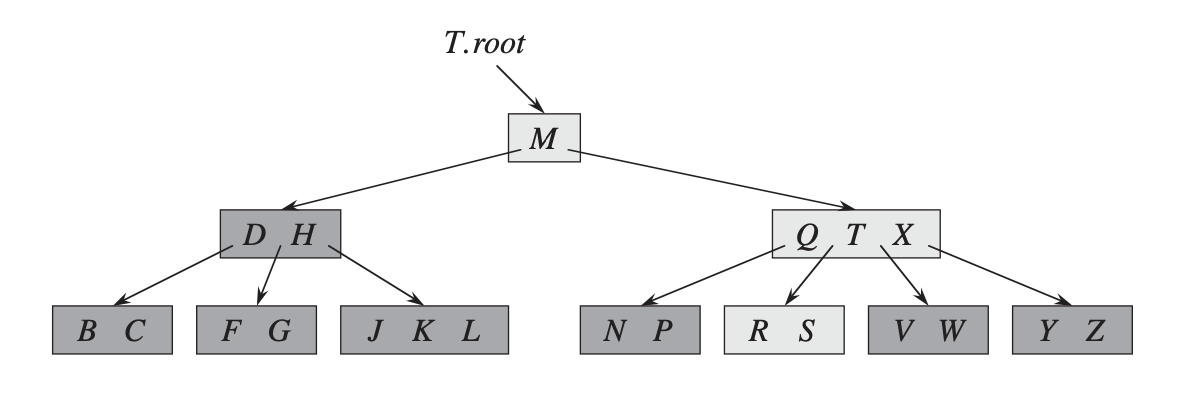
B-Trees

B-Trees are balanced search trees that work well on disks and other secondary storage devices. One of the main differences from a binary search tree is the branching factor. In a binary search tree the branching factor is two, but in a B-Tree it can vary from a few to hundreds. This helps keeping the tree height low which means less nodes to visit. The branching factor is determined by the size of the nodes; usually the size of a disk block, 4 KiB; and the size of the elements stored in the nodes. For example, if a tree has nodes of size 16 KiB and each element is 500 bytes, each node can store 32 elements which then makes it for a branching factor of 32. A tree with these characteristics and a height of 4 levels can store around 1 million elements using just 64 MiB.

By choosing the node size as the same size of a page in a disk it improves the performance when the tree is used as an index for the stored data because multiple items are stored in a single page/node and updates to those elements don’t require random disk seeks which would happen if the number of elements in each node was smaller.

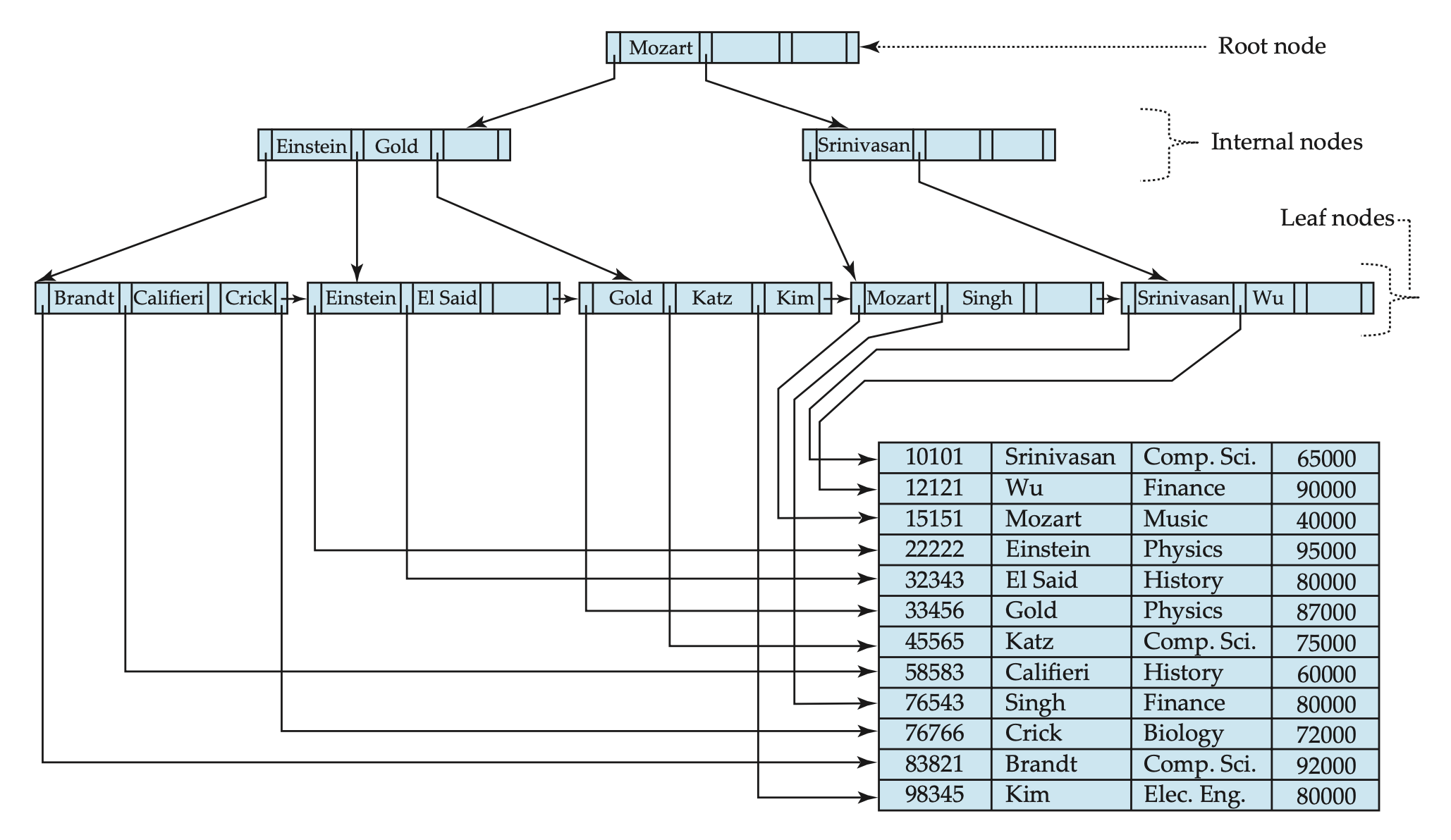
B-Tree

B+-Trees

In B-Trees, every node has the same structure in terms of what information it stores. In B+-Trees, only the leaf nodes store information about the items and the internal nodes are only used for guidance when traversing the tree.

The advantage of that is such that when updates happen to the tree it doesn’t need to immediatelly “travel up” so that parent nodes are updated as well. For example, if an element has been deleted from the tree and it doesn’t require any re-balancing, the internal nodes don’t need to be updated which speeds up the process by eliminating operations. Eventually, when splits and merges of nodes happen the internal nodes will be updated. And even in the case of a deleted key was being used in an internal node, the search would need to go all the way to the leaf nodes to retrieve the desired information so in the end having the internal node with outdated guiding keys doesn’t ruin the traversal.

B+-Tree

References